郑州大学刘凯凯/单崇新《Light: Science & Applications》:碳点中长寿命三重态激子用于含时物理不可克隆函数
物理不可克隆函数(PUF)通过物理实体内部随机的结构单元构建出独一无二的密钥基元,在防伪加密领域发挥着至关重要的作用。PUF可通过力、热、光、电、磁等的物理刺激方式形成唯一性的响应信号,这些响应信号最终被转化为数字化编码,因此,PUF被攻击者破解的难度取决于物理实体单元构建的数字编码的复杂程度。然而,传统PUFs多停留在空间维度,依靠静态的结构差异来生成密钥, 这种方式在编码容量和防伪复杂性上存在天花板,使得基于PUF的防伪加密手段变得不再牢不可破。因此,如何突破这一限制,使其能够应对更加先进的密钥攻击方式,一直是科研界的难题。
研究团队受薛定谔方程中“粒子波函数随时间演化”的启发,作者通过引入具有明亮且长寿命的三重态激子作为块单元的碳点来构造含时物理不可克隆函数(TD-PUFs)。将微观领域的思想引入信息安全领域,开创了全新的含时物理不可克隆函数(TD-PUFs):
引入时间维度:构建的 TD-PUFs 随着时间的推移演变成多个全新的 PUF,PUFs不再局限于空间,而是随时间不断演化,动态生成新的不可克隆模式,有效增加了复杂性和破解难度。
复杂性大幅提升:团队提出像素矩阵函数(Pixel Matrix Function, PMF)用数学形式刻画PUFs在时空维度的演化,从而能够详细分析动态行为和独特的安全特征,其编码容量提高了五个数量级。
用于艺术溯源:研究者还利用碳点构建了30×40 cm²的“动态防伪孔雀画”。随着时间推移,画作的结构和色彩会发生难以预测的变化,既美学独特,又具高度防伪价值。

相关研究成果以“Time-dependent physical unclonable functions by long-lived triplet excitons in carbon dots”为题,发表在《Light: Science & Applications》期刊上。该成果的通讯作者为郑州大学刘凯凯教授和单崇新教授,刘凯凯课题组的博士研究生胡宴伟和曹庆为论文第一作者。
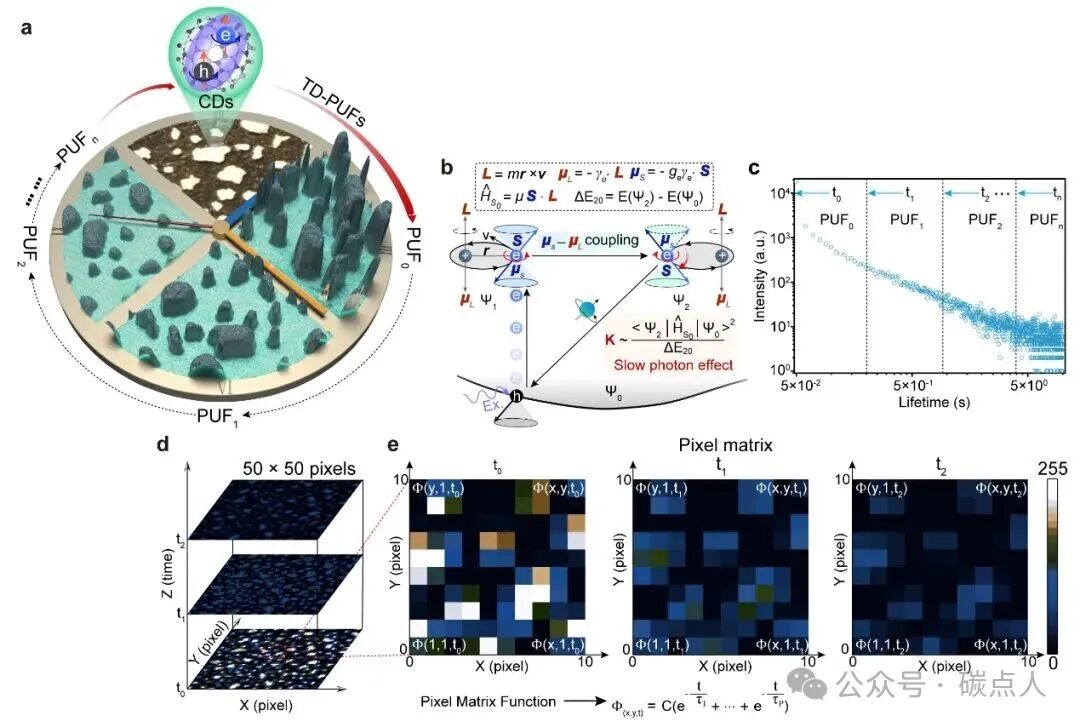
图1. 基于具有三重态激子的CD的TD-PUF示意图和相应的像素矩阵函数。a TD-PUF随时间演化的示意图。b 三重态电子的布居过程和自旋禁阻跃迁引起的慢光子效应示意图。c 室温下365 nm激发下的磷光衰减曲线(寿命)。d TD-PUF 在时间 t0、t1 和 t2 时的灰度值分布图(50 × 50 像素)。e TD-PUF 随时间变化的详细演化过程(局部放大的矩阵数列)以及构建的像素矩阵函数(底部)。
TD-PUF 每个像素内CD的数量和寿命的变化导致了TD-PUF随时间的不同而发生各种变化,TD-PUF 的示意图如图 1 所示。TD-PUF是使用随机分布的磷光CD作为构建单元构建的,读取过程包括三个部分:挑战、响应和数字化。当光源激发后,由于CD的长时间发光特性,TD-PUF会在光源移除后随时间演变为不同的PUF。如图 1a 所示,新生成的 PUF表现出显著的差异,这归因于TD-PUF中每个像素内CD的数量和寿命的变化。在整个 TD-PUF系统中,生成的PUF的数量由时间间隔决定,时间间隔可以从纳秒到秒。因此,CD的寿命和磷光强度在决定 TD-PUF 的功效方面起着关键作用。具体而言,这些特性受自旋轨道耦合 (SOC)和非辐射复合过程控制。SOC促进系间窜越 (ISC),使单重态激子跃迁为长寿命的三重态。由于三重态到单重态跃迁的自旋禁阻性质,辐射衰变显著延长,如图 1b 所示。为了增强这一过程,将重原子掺入CD结构中,以提高SOC强度,从而延长三重态寿命。在365 nm激发下,CD的发光时间延长至10 s,如图1c所示。TD-PUF由PUF0、PUF1、PUF2直至PUFn组成,可以使用时间切片技术系统地构建,时间间隔由快门频率决定。
为了清晰地刻画TD-PUF在时间和空间维度上的演化,提取了同一空间维度内不同时刻t0、t1和t2的PUF,如图1d所示。其中,X轴和Y轴表示TD-PUF的空间坐标,Z轴表示时间维度。随着时间的推移,TD-PUF呈现出不同的结构,彼此之间互不相同。如图1e 所示,我们选取时间t0、t1和t2的TD-PUF(10×10 像素)来展示它们之间的差异和相互关联。为了清晰起见,我们将PUF数字化并标记为二维像素矩阵。
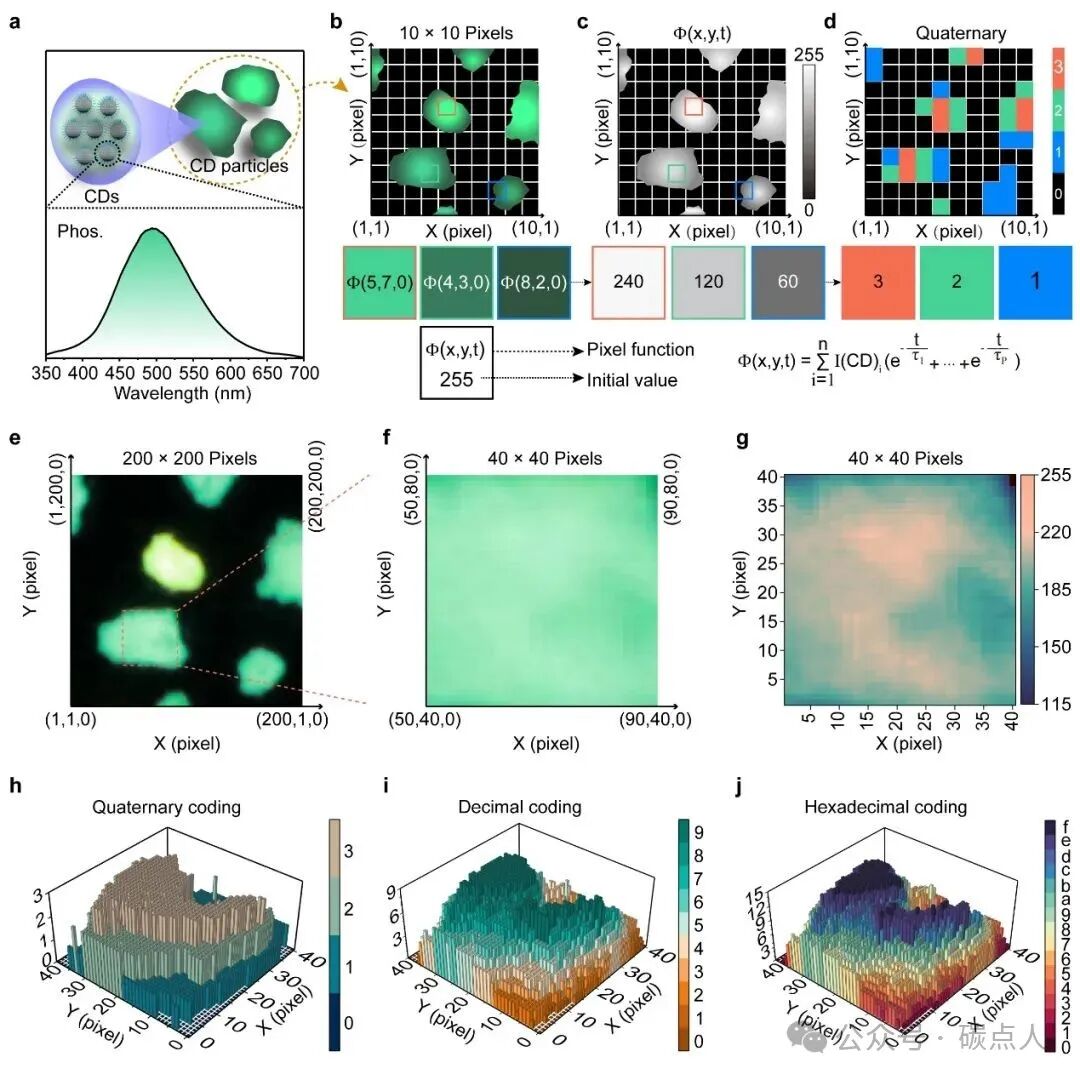
图2. 通过边界条件构建PMF。a CD粒子组装过程示意图以及相应的磷光光谱。b 模拟TD-PUF响应的光学照片(10 × 10像素)。c 相应的灰度图和(d)四进制编码图。e TD-PUF的光响应照片(200 × 200像素)。f 在t = 0 s时截取跨越坐标(50, 40)到(90, 80)的方形区域,得到40 × 40像素的TD-PUF的响应图和(g)相应的灰度图。h-j 40 × 40像素面积的TD-PUF对应的四进制编码、十进制编码和十六进制编码。
CD 颗粒形状和大小的差异源于单个 CD 的随机组装过程。在室温下,在 365 nm 的最佳激发下,CD 的磷光波长峰值位于 500 nm 左右。利用 CD 粒子的形状、磷光和寿命,图 2b展示出了挑战后的 TD-PUF 图。像素内 CD 数量的差异赋予像素不同的发光强度和寿命。为了准确构建描述 TD-PUF 的 PMF,我们需要确定常数 C 的值,该常数 C 是像素内 CD 发光强度的总和,可以通过将发光强度转换为灰度值来获得。以 t = 0 时的三个初始像素值(标记为 (5, 7, 0)、(4, 3, 0) 和 (8, 2, 0))为例说明 PMF 的构建过程,如图 2b 底部所示。TD-PUF 的发光图像被转换为灰度图像(图 2c,顶部)。三个校准像素的灰度值分别确定为240、120和60(图2c下)。通过采用特定阈值,可以将灰度图像数字化为四进制编码(图2d上),其中分配给三个像素的位值分别为3、2和1(图2d下)。随着时间的推移,灰度值由发光强度的变化而变化,时间t可以通过拟合三重态激子的衰减曲线给出。因此,可以通过求解边界条件和拟合发光衰减曲线来构建基于三重态激子发射的TD-PUF的PMF。
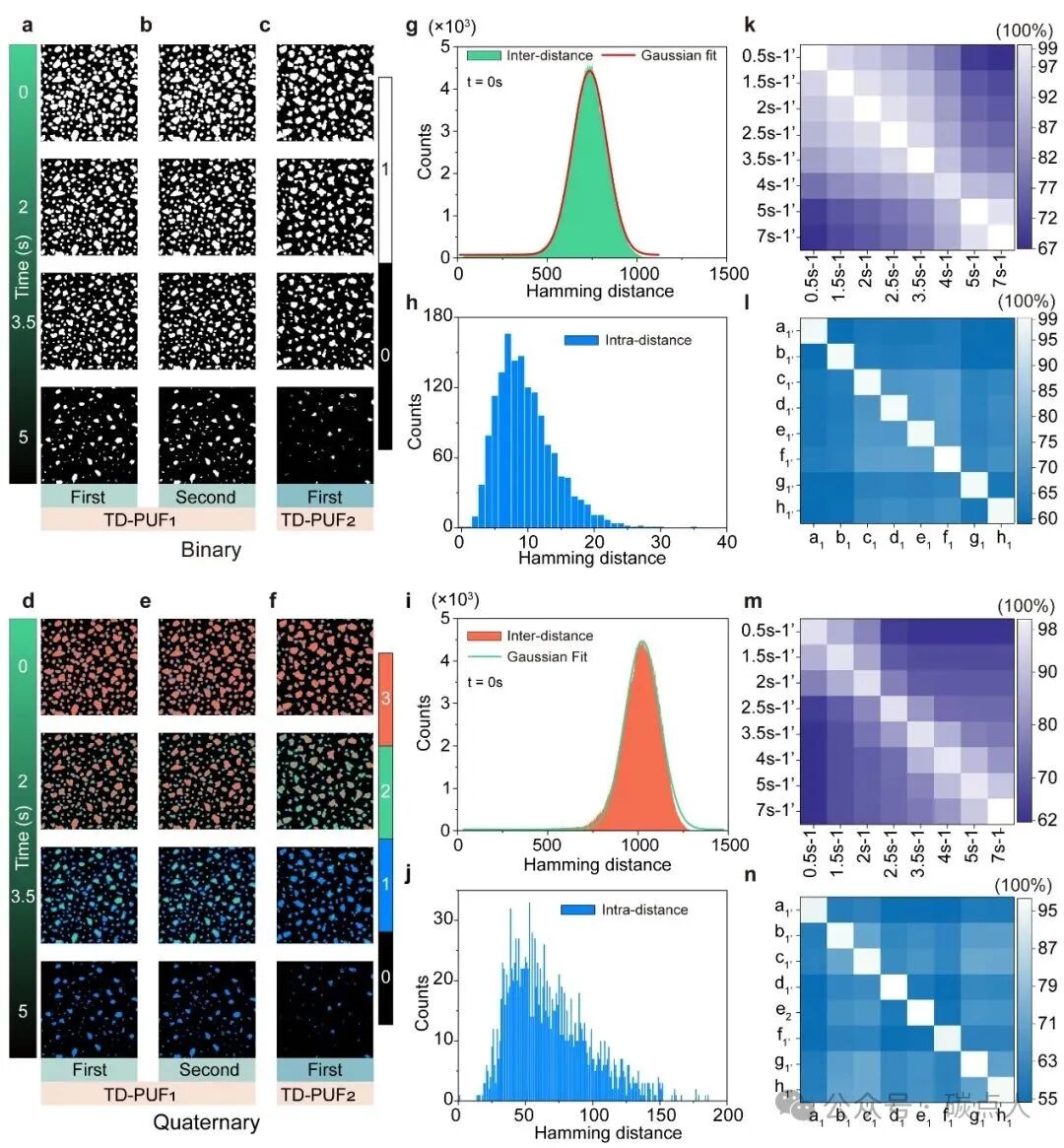
图3. TD-PUF 的性能。在不同时间第一次 (a) 和第二次 (b) 测量的 TD-PUF1 的二进制编码图。c 在不同时间测量的 TD-PUF2 的二进制编码图。在不同时间第一次 (d) 和第二次 (e) 测量的 TD-PUF1 的四进制编码图。f 在不同时间测量的 TD-PUF2 的四进制编码图。g 在 t = 0 s 时测量的 TD-PUF1 的Inter-distance。h 在 t = 0 s 时测量两次的 TD-PUF1 的Intra-distance。i 在 t = 0 s 时测量的具有四进制编码的 TD-PUF1 的Inter-distance。j 在 t = 0 s 时测量两次的具有四进制编码的 TD-PUF1 的Intra-distance。 k 在八个不同时刻测量两次二进制编码的 TD-PUF1 的相似性统计图。l 在 t = 0 s 时测量两次八种不同二进制编码的 TD-PUF 的相似性统计图。m 在八个不同时刻测量两次四进制编码的 TD-PUF1 的相似性统计图。n 在 t = 0 s 时测量两次八种不同四进制编码的 TD-PUF 的相似性统计图。
图3为不同CD粒径构成的TD-PUF的安全性能测试。不同CD粒径构成的TD-PUF具有更高的复杂度和安全性,因此对两个不同CD粒径的TD-PUF分别命名为TD-PUF1和TD-PUF2,在不同时间进行测量,然后将其转化为二进制编码和四进制编码进行分析,如图3a-f所示。随后,我们在 t = 0 s 时通过二进制和四进制编码对 TD-PUF 进行了唯一性分析,如图 3g,i 所示。根据理论预期,间距结果遵循二项分布定律,其中汉明间距为 750 表现出最高的出现概率(代表总位数的一半)。为了消除偶然性,我们选取了8个PUF,在t=0.5s时测量两次,进行分析比较,。值得注意的是,在同一时刻测量的同一个PUF的测量结果表现出显著的可重复性。此外,我们在t=0.5s到t=7s的时间内对TD-PUF进行了两次测量,通过成对比较获得了64个相似性指标值。相应的二进制和四元统计结果如图3k、m所示,表明了较高的可重复性和唯一性。我们还对八个不同的1500×1500像素的PUF进行了测量,比较了t = 0s时两次测量的结果,得到了64个相似度指标值,如图3l,n所示比较结果表明,在同一时刻测量两次的同一PUF表现出较高的相似度指标值,而不同PUF以及在不同时刻测量的同一PUF则表现出较低的相似度指标值。
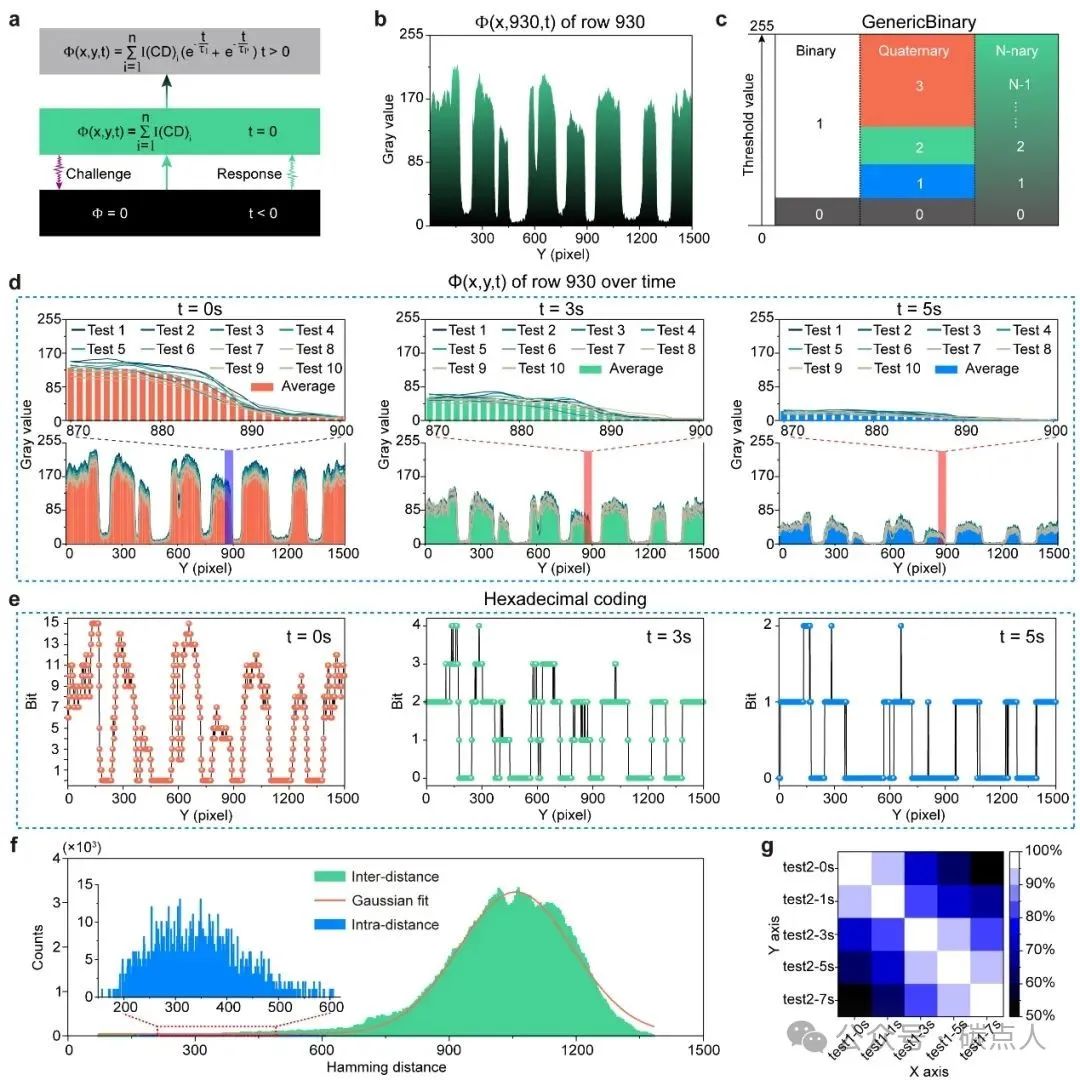
图4. 通过时间切片实现的N进制TD-PUF。a 光激发挑战前后TD-PUF的PMF流程图。b t = 0 s时TD-PUF沿(x, 930)轴的PMF。c 通过选择适当的阈值,从二进制、四进制到N进制编码的示意图。d 分别在t = 0 s、3 s和5 s,在相同激发条件下测量10次TD-PUF的PMF。e 分别在t = 0 s、3 s和5 s,对10次测量取平均值的PMF对应的十六进制编码。f 十六进制编码的TD-PUF的Inter-distance和Intra-distance。g TD-PUF在五个不同时刻两次重复测量后的相似性统计结果。
与传统PUF相比,TD-PUF除了空间维度外,还整合了时间维度,呈现出时间演化特性。在时间t < 0时,PMF等于零;经过挑战后,PMF在t = 0时表现出光响应;随后,PMF随时间呈指数衰减,如图4a所示。为了更清楚地解释TD-PUF内每个像素的响应如何随时间变化,我们从1500×1500像素的TD-PUF中随机选择了一行数据进行分析,PMF如图4b所示。这里,像素内CD的强度被转换为灰度值(该值位于0到255的范围内)。图 4c 描述了从生成灰度值数据到其转换为 N 进制编码的过程。我们采用单个阈值(30)生成二进制编码,三个阈值(30、150 和 200)产生四进制编码,以及多个阈值产生 N 进制编码。随着时间的推移,四进制编码随着灰度值在相同阈值下降低而演变。我们在相同的激励挑战下重复了 TD-PUF 的响应测试 10 次,以避免意外变化,t = 0 s、3 s 和 5 s 时的灰度值结果如图 4d 所示,显示出较高的可靠性和一致性。图 4e 分别显示了 t = 0 s、3 s 和 5 s 时十六进制编码的编码统计结果。结果表明,十六进制编码也会随时间随机演变,从而解释了原始 PUF 能够生成新 PUF 的原因。最后,十六进制编码 TD-PUF 的安全性表征结果也证实了其优异的性能,如图 4f 所示。图 4g是同一时间间隔变化下 TD-PUF 两次重复测试结果的相似性。结果表明,由 TD-PUF 衍生的新 PUF 会随时间随机变化,结果突显了 TD-PUF 在关键评估指标上的卓越性能。
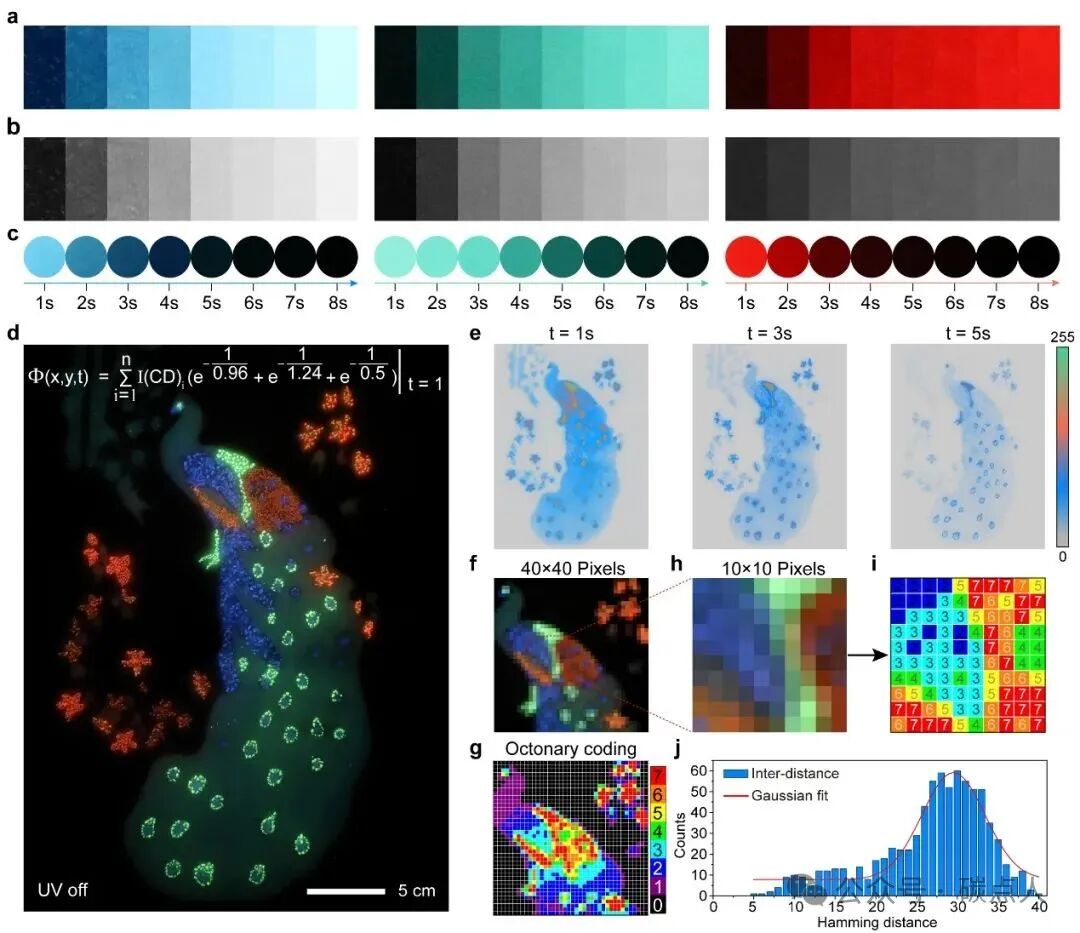
图5. TD-PUFs技术的应用。a 用三种不同浓度的CD制备的薄膜的磷光图像。b 磷光图像对应的灰度图像。c 在不同时间拍摄的三张CD的磷光照片。d 在t = 1 s时TD-PUF绘画的光学响应照片。e 在t = 1 s、3 s、5 s时TD-PUF绘画的伪彩图像。f 从孔雀画中剪切下的40×40像素区域的光学照片。g 相应的八进制编码图。h 10×10像素区域的放大详细光学照片。i 10×10像素区域中孔雀图案对应的八进制编码图。j 40×40像素区域中孔雀图案的Intra-distance。
TD-PUF由于时间维度的引入表现出巨大的信息存储能力,使得该技术非常适合于信息存储和防伪。利用TD-PUF技术已经制作出了多种防伪标签,可以粘贴在重要且贵重物品的表面。此外,我们进一步扩展了TD-PUF技术在共生防伪绘画中的应用,如图5所示。我们选择了三种不同寿命和磷光性的CD用于制备TD-PUF绘画。图5a为不同CD含量薄膜的磷光照片(照片拍摄于t=1 s时刻),并将其转化为灰阶图像进行分析(图5b)。单位体积内 CD 含量增加,灰度值也随之增加,表明它们可以用于多层次、生动的绘画。此外,它们表现出随时间变化的发射特性,发射持续时间超过 8 秒,表明它们具有用于 TD-PUF 绘画的潜力。通过蚀刻技术创作了 TD-PUF 孔雀图案画。CD 的鲜艳发射和多样化的寿命赋予画作更丰富的变化,使其具有很强的防伪性能。该画作随着时间的推移产生视觉响应,仿佛栩栩如生。CD 的活跃三重态激子发射和不同的寿命使得画作随着时间的推移呈现出动态且视觉上引人注目的变化,使其具有极强的防伪性。
本工作提出并展示了TD-PUF技术,时间维度的引入使其具备了动态、灵活的防伪、信息存储和可视化表达能力。以长寿命、明亮的三重态激子的CD作为构建TD-PUF的基石,打破了空间限制,增加了被攻击的难度。此外,作者通过求解边界条件构建了PMF,用于描述TD-PUF随时间的变化。此外,作者通过灵活的标记展示了TD-PUF的多功能性,并强调了其在贵重物品防伪方面的应用。最后,作者展示了TD-PUF的绘画,CD的鲜艳发光和多样化的寿命赋予绘画更丰富的变化,使其具有很强的抗伪造能力。本研究中TD-PUF技术的引入,标志着传统PUF摆脱了空间上的限制,为PUF在时间维度上的重大发展铺平了道路。
论文链接:
Yan-Wei Hu, Qing Cao, Shi-Yu Song, Yuan Sun, Ya-Chuan Liang, Wen-Bo Zhao, Chao-Fan Lv, Chong-Xin Shan & Kai-Kai Liu. Time-dependent physical unclonable functions by long-lived triplet excitons in carbon dots. Light Sci. Appl. 14, 283 (2025).
https://doi.org/10.1038/s41377-025-01940-9